【土木の面積計算】は簡単？計算方法を分かりやすく解説！公式を覚えれば分かりやすい！

こんにちは！土木ブロガーの監督やっくんです！

建設業に携わっている方で、「多角形の面積計算方法が分からない」「計算式が知りたい」と悩んでいませんか。

作業現場では、路盤や舗装の面積を出来形測定するのに、面積を確認する場面がいくつもあります。

今回の記事は、そんな『面積の計算方法』について解説していきます。

舗装の出来形を測るのに面積の計算方法を知りたいな～

新人さん

やっくん

ヘロンの公式(三辺法)を使って計算するんだよ！

ヘロン公式による計算方法

計算のポイントは以下の通りです。

三角形に分割する

1.例えば以下のような形の展開図があったとします

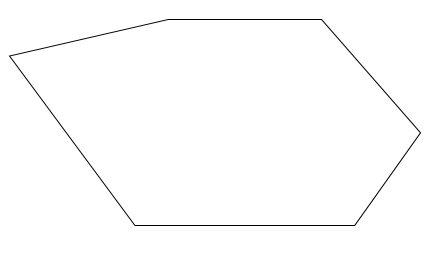
2.線(赤線)を引き、三角形に分割する(4つの分割)

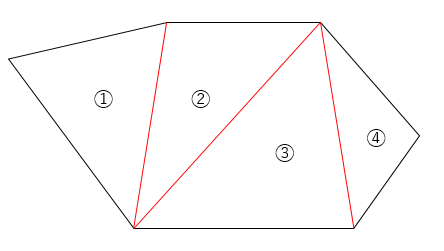
三斜法より三辺法のが早く計算できる

1.三斜法で面積を求める場合

三斜法とは、多角形である三角形を分割し、それぞれの三角形について底辺×高さによって面積を求め、それらの三角形の面積の合計によって目的とする土地全体の面積を求めるものです。

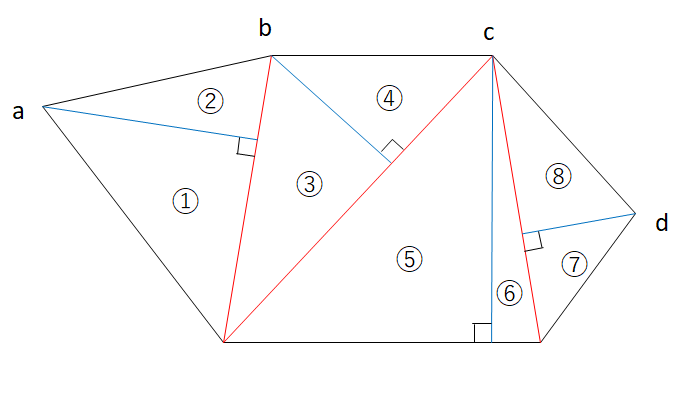
三角形の頂点a、b、c、dから垂線(青線)を引き、直角三角形にする(8つに分割)。

それぞれ底辺×高さ×$\frac{1}{2}$で三角形の面積を求め、最後に合計します。

しかし、この方法だと垂線を引き直角三角形にするので手間が多くなる。

2.そこでオススメなのがヘロン公式(三辺法)で求める方法です

ヘロンの公式

ヘロンの公式(三辺法)とは3辺の長さが分かっている三角形の面積を求める公式です。

例として③の面積を計算して見ましょう！

面積はヘロンの公式で求めることができます。

三辺の長さがA、B、C、の三角形の面積Sは、

$t＝\frac{A+B+C}{2}$

と置くと

$S=\sqrt{t(t-A)(t-B)(t-C)}$

で計算できる。

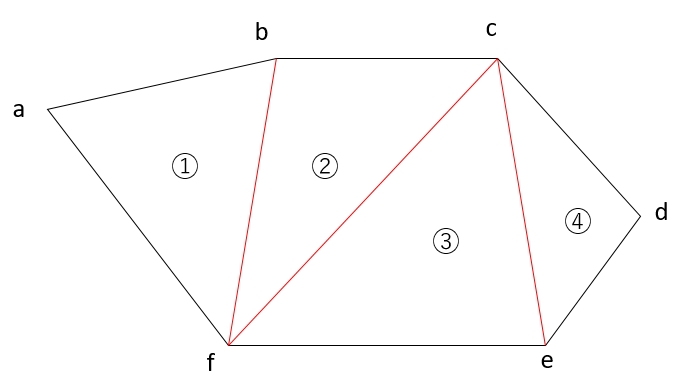
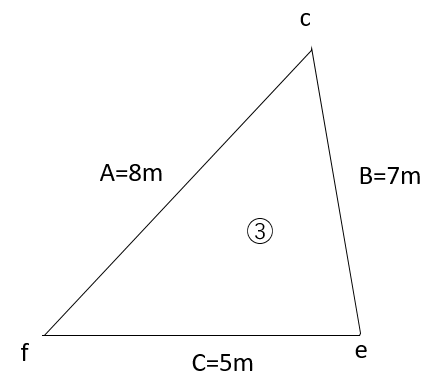
例えばA=8、B=7，C=5としてヘロンの公式を用いる。

まずtを求める。

$t＝\frac{8+7+5}{2}$=10

そして面積を計算する。

$S=\sqrt{10(10-8)(10-7)((10-5)}$=$\sqrt{10・2・3・5}$=$10\sqrt3$=17.3205・・・・小数に直すとこのように求めることができます。

まとめ

実際に建設現場で、面積を管理する時は、ルートを小数にしないと分かりづらいです！面積の計算には関数電卓があると便利ですね～

カシオ｜CASIO 関数電卓 fx-JP500-N [10桁][FXJP500N]

posted with カエレバ

 

楽天市場で探す

Amazonで探す

Yahooショッピングで探す

 

本ブログでは建設現場でよく使う土方カーブの出し方と土量の変化率についてを紹介しています。以下の記事を本記事と合わせて読んで みてください。

計算の仕方がが分かるよ～！

【土方カーブrの出し方】？！建設現場で使える公式！覚えれば分かりやすい！
土量の変化率って何！？一級土木施工管理技士が解説